1.5 KiB
1.5 KiB
Introduction
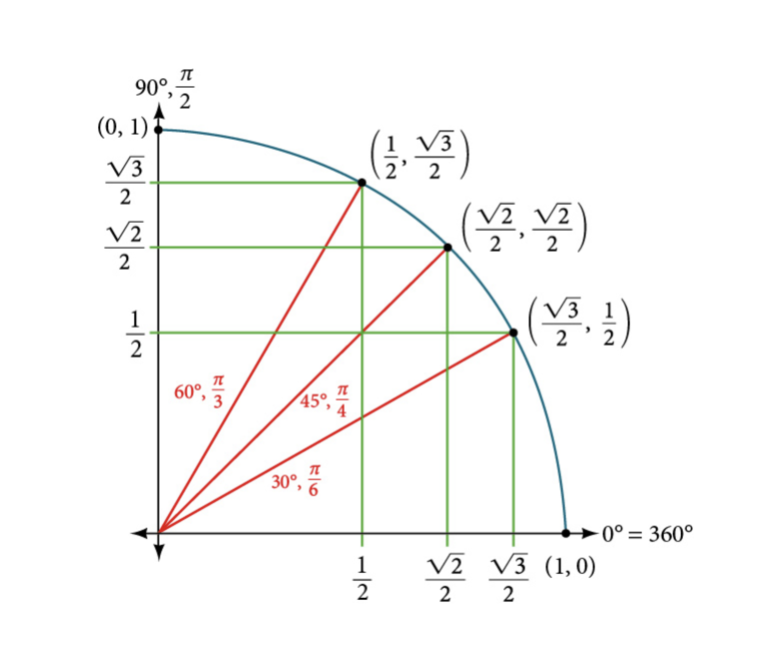
The unit circle has a center a (0, 0), and a radius of 1 with no defined unit.
Sine and cosine can be used to find the coordinates of specific points on the unit circle.
Sine likes y, and cosine likes x.
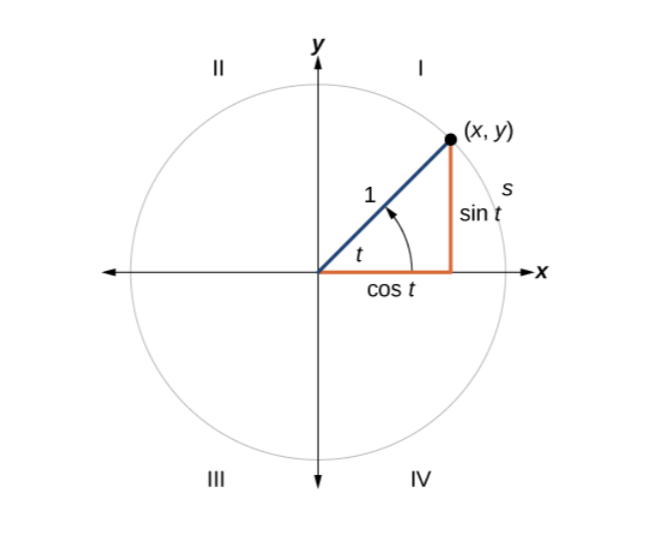 When sine is positive, the
When sine is positive, the y value is positive. When x is positive, the cosine is positive.
cos(\theta) = x sin(\theta) = y Sine and Cosine
| Angle | 0 |
\frac{\pi}{6} or 30 \degree |
\frac{\pi}{4} or 45\degree |
\frac{\pi}{2} or 90\degree |
|---|---|---|---|---|
| Cosine | 1 | \frac{\sqrt{3}}{2} |
\frac{\sqrt{2}}{2} |
0 |
| Sine | 0 | \frac{1}{2} |
\frac{\sqrt{2}}{2} |
1 |
The Pythagorean Identity
The Pythagorean identity expresses the Pythagorean theorem in terms of trigonometric functions. It's a basic relation between the sine and cosine functions.
sin^2 \theta + cos^2 \theta = 1 Definitions
| Term | Description |
|---|---|
\theta (theta) |
Theta refers to the angle measure in a unit circle. |
s |
s is used to the length of the arc created by angle \theta on the circle. |