notes/education/computer engineering/ECE2700/Binary Logic.md

History of Boolean Algebra

• In 1849, George Boole published a scheme for describing logical thought and reasoning
• In the 1930s, Claude Shannon applied Boolean algebra to describe circuits built with switches
• Boolean algebra provides the theoretical foundation for digital design

Properties of Boolean Algebra

Number	Col. A	Col. A Description	Col. B	Col. B Description
1.	0 \cdot 0 = 0		1 + 1 = 1
2.	1 \cdot 1 = 1		0 + 0 = 0
3.	0 \cdot 1 = 1 \cdot 0 = 0		1 + 0 = 0 + 1 = 1
4.	if x = 0 then \overline{x} = 1		if x = 1 then \overline{x} = 0
5.	x \cdot 0 = 0		x + 1 = 1
6.	x \cdot 1 = x		x + 0 = x
7.	x \cdot x = x		x + x = x
8.	x \cdot \overline{x} = 0		$x + \overline{x} = 1
9.	\overline{\overline{x}} = x
10. Commutative	x \cdot y = y \cdot x		x + y = y + x
11. Associative	x \cdot (y \cdot z) = (x \cdot y) \cdot z		x + (y + z) = (x + y) +z
12. Distributive	x \cdot (y +z) = x \cdot y + x \cdot z		x + y \cdot z = (x + y) \cdot (x + z
13. Absorption	x + x \cdot y = x		x \cdot (x + y) = x
14. Combining	x \cdot y + x \cdot \overline{y} = x		(x + y) \cdot (x + \overline{y}) = x
15. DeMorgan's Theorem	\overline{x \cdot y} = \overline{x} + \overline{y}		x + y = \overline{x} \cdot \overline{y}
16.	x + \overline{x} \cdot y = x + y		x \cdot (\overline{x} + y) = x \cdot y
17. Consensus	x \cdot y + y \cdot z + \overline{x} \cdot z = x \cdot y + \overline{x} \cdot z		(x + y) \cdot (y + z) \cdot (\overline{x} + z) = (x + y) \cdot (\overline{x} + z)

Synthesis

In the context of binary logic, synthesis refers to the act of creating a boolean expression that evaluates to match a given truth table.

This is done by creating a product term for each entry in the table that has an output of 1, that also evaluates to 1, then ORing each product term together and then simplifying.

Example:

Given the below truth table, synthesize a boolean expression that corresponds.

x_1	x_2	f(x_1, x_2)
0	0	1
0	1	1
1	0	0
1	1	1

• f(0, 0) evaluates to true with the expression \overline{x}_1 \cdot \overline{x}_2
• f(0, 1) evaluates to true with the expression \overline{x}_1\cdot x_2
• f(1, 0) should provide an output of zero, so that can be ignored
• f(1, 1) evaluates to true with the expression x_1 \cdot x_2 ORing all of the above expression together, we get:

f(x_1, x_2) = \overline{x}_1\overline{x}_2 + \overline{x}_1 x_2 + x_1x_2

\begin{multline}
= x_1x_2 \\
= x
\end{multline}

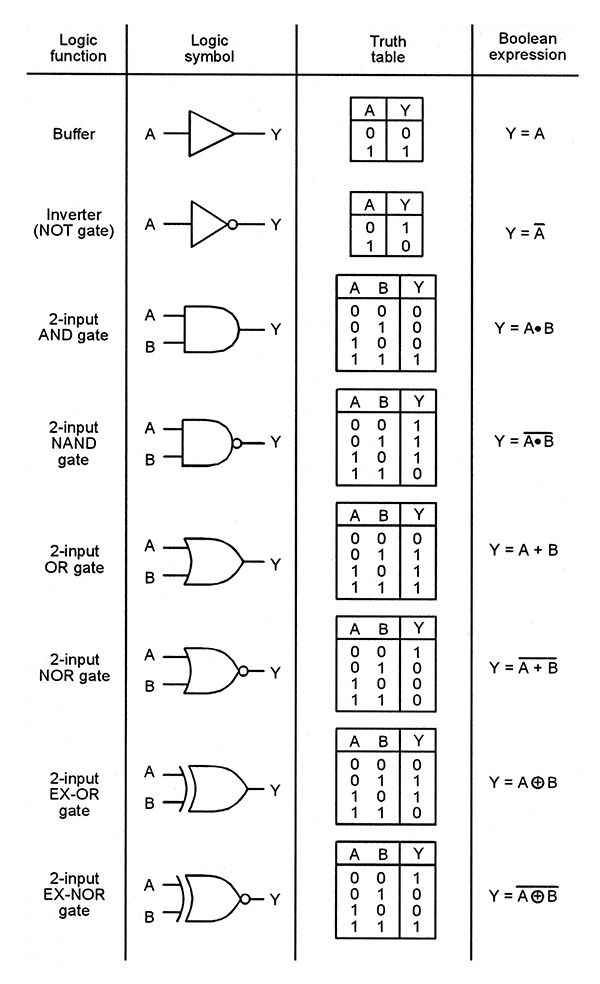
Logic Gates

NOT Gate

A binary NOT gate has a single input, and inverts that input (output is not the input).

Truth Table

x	y
0	1
1	0

Mathematical Expression

A NOT operation is mathematically expressed using a bar:

y = \bar{x}

AND Gate

An AND gate will only output a 1 if both inputs are a one (input one and input two are enabled).

Truth Table

x_1	x_2	y
0	0	0
0	1	0
1	0	0
1	1	1

Mathematical Expression

An AND operation is mathematically expressed using a times symbol, or with no symbol at all:

y = x_1 \cdot x_2 = x_1x_2

NAND Gate

A NAND gate outputs a 1 unless both inputs are enabled (input one and input two are not enabled).

Truth Table

x_1	x_2	y
0	0	1
0	1	1
1	0	1
1	1	0

Mathematical Expression

A NAND operation is mathematically expressed using a bar over an AND operation:

y = \overline{x_1 \cdot x_2}

OR Gate

An OR gate outputs a 1 if either or both inputs are enabled (if input one or input two is enabled).

Truth Table

x_1	x_2	y
0	0	0
0	1	1
1	0	1
1	1	1

Mathematical Expression

A mathematical OR is notated with a + symbol.

y = x_1 + x_2

NOR Gate

A NOR gate outputs a one if neither gate is enabled.

Truth Table

x_1	x_2	y_1
0	0	1
0	1	0
1	0	0
1	1	0

Mathematical Expression

A NOR operation is expressed using a bar over an OR operation.

y = \overline{x_1 + x_2}

XOR Gate

An XOR gate is on if one input is enabled, but not both (exclusively one or the other).

Truth Table

x_1	x_2	y
0	0	0
0	1	1
1	0	1
1	1	0

Mathematical Expression

An XOR operation is expressed using a circle around an addition symbol:

y = x_1 \oplus x_2

XNOR Gate

An XNOR gate is on if neither input is enabled, or both inputs are enabled.

Truth Table

x_1	x_2	y
0	0	1
0	1	0
1	0	0
1	1	1

Mathematical Expression

An XNOR operation is expressed using a bar over an XOR operation:

y = \overline{x_1 \oplus x_2}