notes/education/math/MATH1060 (trig)/Graphing.md

Sine/Cosine

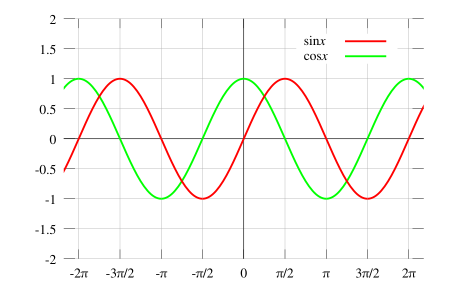
Given the above graph:

• At the origin, sin(x) = 0 and cos(x) = 1
• A full wavelength takes 2\pi

Manipulation

Formula	Movement
y = cos(x) - 1	Vertical shift down by 1
y = 2cos(x)	Vertical stretch by a factor of 2
y = -cos(x)	Flip over x axis
y = cos(2x)	Horizontal shrink by a factor of 2

Periodic Functions

A function is considered periodic if it repeats itself at even intervals, where each interval is a complete cycle, referred to as a period.

Sinusoidal Functions

A function that has the same shape as a sine or cosine wave is known as a sinusoidal function.

There are 4 general functions:

$$A * sin(B*x - C) + D$$	y = A * cos(B*x -c) + D$$
y = A * sin(B(x - \frac{C}{B})) + D	y = A*cos(B(x - \frac{C}{B})) + D$$

How to find the:

• Amplitude: |A|
• Period: \frac{2\pi}{B}
• Phase shift: \frac{C}{|B|}
• Vertical shift: D

 y = A * \sin(B(x-\frac{C}{B})) 

Tangent

 y = tan(x)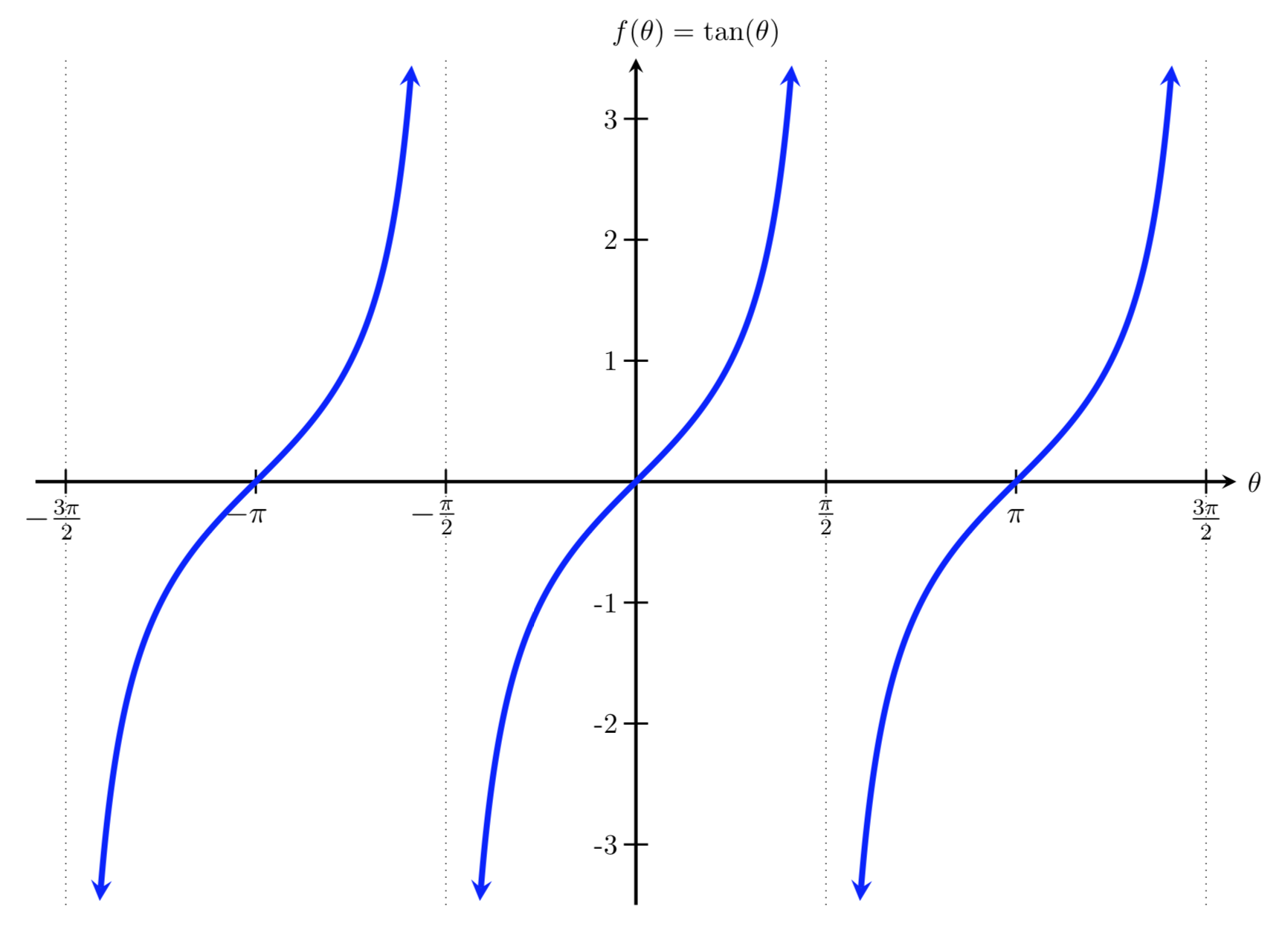 

To find relative points to create the above graph, you can use the unit circle:

If tan(x) = \frac{sin(x)}{cos(x}), then:

sin(0) = 0	cos(0) = 1	tan(0) = \frac{cos(0)}{sin(0)} = \frac{0}{1} =0
sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	tan(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}/\frac{\sqrt{2}}{2} = 1
sin(\frac{\pi}{2}) = 1	cos(\frac{\pi}{2}) = 0	tan(\frac{\pi}{2}) = \frac{1}{0} = DNF
Interpreting the above table:

• When x = 0, y = 0
• When x = \frac{\pi}{4}, y = 1
• When x = \frac{\pi}{2}, there's an asymptote

Without any transformations applied, the period of tan(x) = \pi. Because tan is an odd function, tan(-x) = -tan(x).

Cotangent

 y = cot(x) 

To find relative points to create the above graph, you can use the unit circle:

If cot(x) = \frac{cos(x)}{sin(x)}, then:

sin(0) = 0	cos(0) = 1	cot(0) = \frac{sin(0)}{cos(0)} = \frac{1}{0} = DNF
sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cot(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}/\frac{\sqrt{2}}{2} = 1
sin(\frac{\pi}{2}) = 1	cos(\frac{\pi}{2}) = 0	tan(\frac{\pi}{2}) = \frac{1}{0} = DNF

Without any transformations applied, the period of cot(x) = \pi. Because cot is an odd function, cot(-x) = -cot(x).

Features of Tangent and Cotangent

Given the form y = A\tan(Bx - C) + D (the same applies for \cot)

• The stretching factor is |A|
• The period is \frac{\pi}{|B|}
• The domain of tan is all of x, where x \ne \frac{C}{B} + \frac{\pi}{2} + {\pi}{|B|}k, where k is an integer. (everywhere but the asymptotes)
• The domain of cot is all of x, where x \ne \frac{C}{B} + \frac{\pi}{|B|}k, where k is an integer (everywhere but the asymptotes)
• The range of both is (-\infty, \infty)
• The phase shift is \frac{C}{B}
• The vertical shift is D

Secant

 y = \sec(x) 

 sec(x) = \frac{1}{\cos{x}} 

Because secant is the reciprocal of cosine, when \cos{x} = 0, then secant is undefined. $|\cos$| is never greater than 1, so secant is never less than 1 in absolute value. When the graph of cosine crosses the x axis, an asymptote for a matching graph of secant will appear there.

The general form of secant is:

 y = A\sec(B{x} - C) + D 

A, B, C, and D will have similar meanings to the secant function as they did to the sine and cosine functions.

Cosecant

 y = \csc(x) 

 \csc(x) = \frac{1}{\sin(x)} 

Because cosecant is the reciprocal of sine, when \sin{x} = 0, then cosecant is undefined. $|\sin$| is never greater than 1, so secant is never less than 1 in absolute value. When the graph of sine crosses the x axis, an asymptote for a matching graph of cosecant will appear there.

The general form of cosecant is:

 y = A\csc(B{x} - C) + D 

A, B, C, and D will have similar meanings to the cosecant function as they did to the sine and cosine functions.

Features of Secant and Cosecant

• The stretching factor is |A|
• The period is \frac{2\pi}{|B|}
• The domain of secant is all x, where x \ne \frac{C}{B} + \frac{\pi}{2} + \frac{\pi}{|B|}k, where k is an integer. (Every half period + phase shift is where asymptotes appear)
• The domain of cosecant is all x, where x \ne \frac{C}{B} + \frac{\pi}{|B|}k, where k is an integer.
• The range is (\infty, -|A| +D]\cup [|A| + D], \infty)
• The vertical asymptotes of secant occur at x = \frac{C}{B} + \frac{\pi}{2} + \frac{\pi}{2} + \frac{\pi}{|B|}k, where k is an integer.
• The vertical asymptotes of cosecant occur at x = \frac{C}{B} + \frac{\pi}{|B|}k, where k is an integer.
• The vertical shift is D.

Inverse Functions

For any one to one function f(x) = y, a function f^{-1}(y) = x). A function is considered one-to-one if every input only has one output, and every output can only be created from a single input.

The inverse of a trig function is denoted as sin^{-1}, or arcsin respectively.

The inverse of a trig function is not the same as the reciprocal of a trig function, \frac{1}{sin} is not the same as sin^{-1}.

• The domain of f is the range of f^{-1}.
• The range of f is the domain of f^{-1}.

Trig functions	Inverse trig functions
Domain: Angle measures	Domain: Ratio of sides of a triangle
Range: Ratio of sides of a triangle	Range: Angle Measure

• To find the inverse of sin, you need to restrict the domain to [-\frac{\pi}{2}, \frac{\pi}{2}]
• To find the inverse of cos, you need to restrict the domain to [0, \pi]
• To find the inverse of tangent, you need to restrict the domain to (-\frac{\pi}{2}, \frac{\pi}{2}).

The graphs of an inverse function can be found by taking the graph of f, and flipping it over the line y=x.

Examples

Given -2\tan(\pi*x + \pi) - 1

A = -2, B = \pi, C = -\pi, D = -1

Identify the vertical stretch/compress factor, period, phase shift, and vertical shift of the function y = 4\sec(\frac{\pi}{3}x - \frac{\pi}{2}) + 1

A = 4, B = \frac{\pi}{3}, C = \frac{\pi}{2}, D = 4

Vertical stretch: $|4| = 4$ Period: $\frac{2\pi}{\frac{\pi}{3}} = \frac{2\pi}{1} * \frac{3}{\pi} = 6$ Phase shift: $\dfrac{\frac{\pi}{2}}{\frac{\pi}{3}} = \frac{3}{2}$ Vertical shift: 1

Transformation	Equation
Stretch	\|-2\| = 2
Period	\frac{\pi}{\|\pi\|} = 1
Phase shift	\frac{-\pi}{\pi} = -1
Vertical shift	-1

Evaluate \arccos{\frac{1}{2}} using the unit circle.

Taking the inverse of the above function, we get this. Because the domain of cos ranges from 0 to \pi inclusive, the answer is going to be in quadrant 1 or quadrant 2.

 cos(x) = \frac{1}{2}