notes/education/math/MATH1060 (trig)/Graphing.md

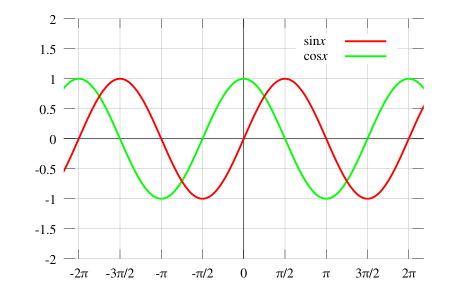
Sine/Cosine

Given the above graph:

• At the origin, sin(x) = 0 and cos(x) = 1
• A full wavelength takes 2\pi

Manipulation

Formula	Movement
y = cos(x) - 1	Vertical shift down by 1
y = 2cos(x)	Vertical stretch by a factor of 2
y = -cos(x)	Flip over x axis
y = cos(2x)	Horizontal shrink by a factor of 2

Periodic Functions

A function is considered periodic if it repeats itself at even intervals, where each interval is a complete cycle, referred to as a period.

Sinusoidal Functions

A function that has the same shape as a sine or cosine wave is known as a sinusoidal function.

There are 4 general functions:

A * sin(B*x - C) + D	y = A * cos(B*x -c) + D
y = A * sin(B(x - \frac{C}{B})) + D	y = A*cos(B(x - \frac{C}{B})) + D

How to find the:

• Amplitude: |A|
• Period: \frac{2\pi}{B}
• Phase shift: \frac{C}{|B|}
• Vertical shift: D

y = A * \sin(B(x-\frac{C}{B}))

Tangent

y = tan(x)

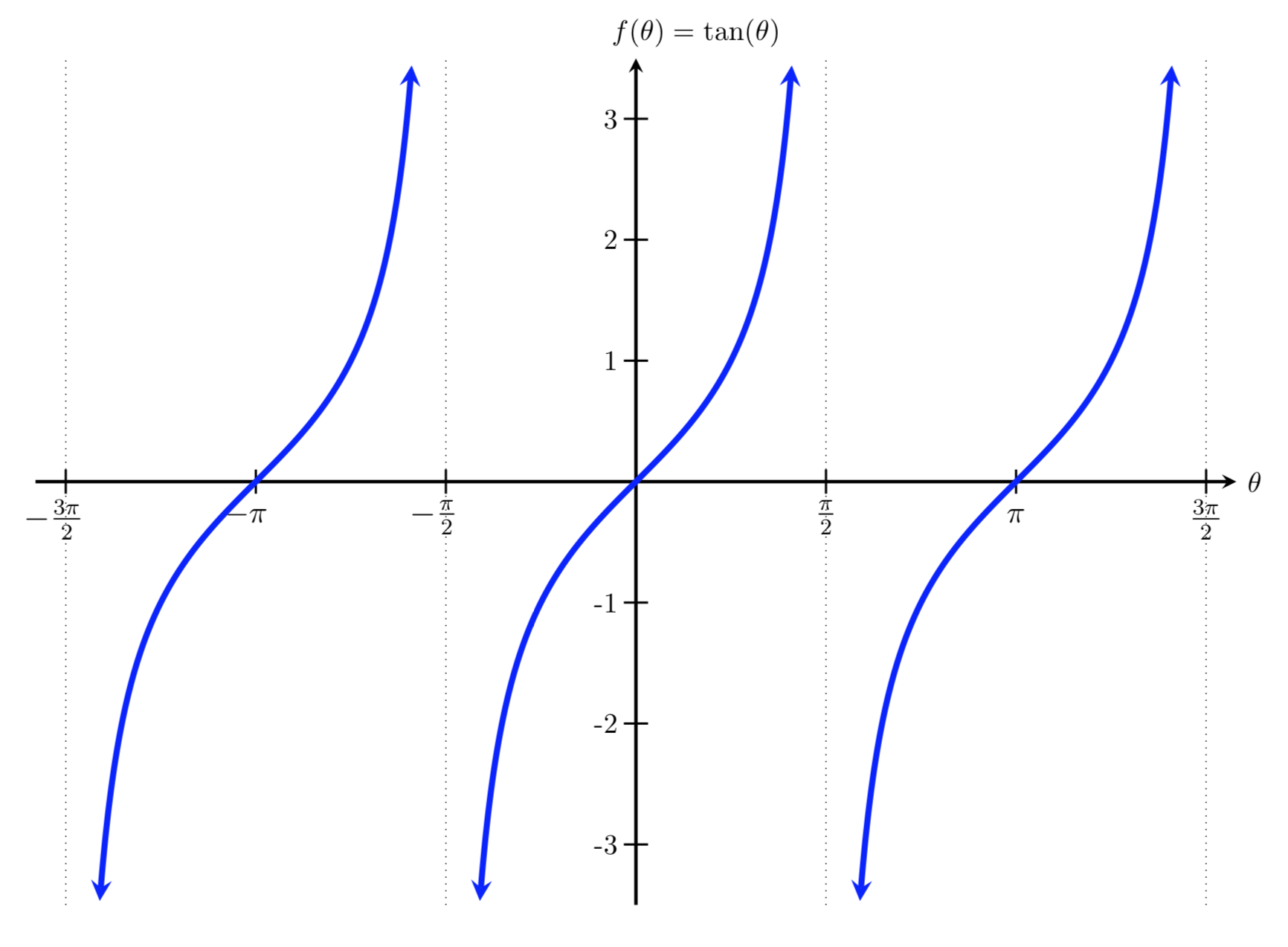To find relative points to create the above graph, you can use the unit circle:

If tan(x) = \frac{sin(x)}{cos(x}), then:

sin(0) = 0	cos(0) = 1	tan(0) = \frac{cos(0)}{sin(0)} = \frac{0}{1} =0
sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	tan(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}/\frac{\sqrt{2}}{2} = 1
sin(\frac{\pi}{2}) = 1	cos(\frac{\pi}{2}) = 0	tan(\frac{\pi}{2}) = \frac{1}{0} = DNF
Interpreting the above table:

• When x = 0, y = 0
• When x = \frac{\pi}{4}, y = 1
• When x = \frac{\pi}{2}, there's an asymptote

Without any transformations applied, the period of tan(x) = 1. Because tan is an odd function, tan(-x) = -tan(x).

Cotangent

y = cot(x)

To find relative points to create the above graph, you can use the unit circle:

If cot(x) = \frac{cos(x)}{sin(x)}, then:

sin(0) = 0	cos(0) = 1	cot(0) = \frac{sin(0)}{cos(0)} = \frac{1}{0} = DNF
sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}	cot(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}/\frac{\sqrt{2}}{2} = 1
sin(\frac{\pi}{2}) = 1	cos(\frac{\pi}{2}) = 0	tan(\frac{\pi}{2}) = \frac{1}{0} = DNF