notes/education/computer engineering/ECE2700/Binary Logic.md

Properties of Boolean Algebra

Number	Col. A	Col. A Description	Col. B	Col. B Description
1.	0 \cdot 0 = 0		1 + 1 = 1
2.	1 \cdot 1 = 1		0 + 0 = 0
3.	0 \cdot 1 = 1 \cdot 0 = 0		1 + 0 = 0 + 1 = 1
4.	if x = 0 then \overline{x} = 1		if x = 1 then \overline{x} = 0
5.	x \cdot 0 = 0		x + 1 = 1
6.	x \cdot 1 = x		x + 0 = x
7.	x \cdot x = x		x + x = x
8.	x \cdot \overline{x} = 0		$x + \overline{x} = 1
9.	$\overline{\overline{x}} =
10.
11.
12.
13.
14.
15.
16.
17.

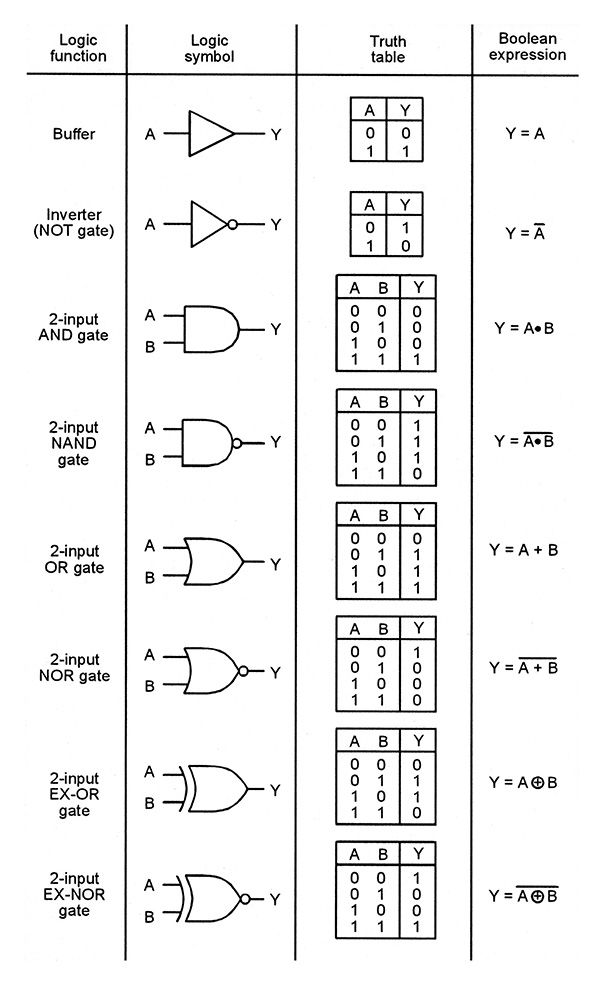
Logic Gates

NOT Gate

A binary NOT gate has a single input, and inverts that input (output is not the input).

Truth Table

x	y
0	1
1	0

Mathematical Expression

A NOT operation is mathematically expressed using a bar:

 y = \bar{x} 

AND Gate

An AND gate will only output a 1 if both inputs are a one (input one and input two are enabled).

Truth Table

x_1	x_2	y
0	0	0
0	1	0
1	0	0
1	1	1

Mathematical Expression

An AND operation is mathematically expressed using a times symbol, or with no symbol at all:

 y = x_1 \cdot x_2 = x_1x_2

NAND Gate

A NAND gate outputs a 1 unless both inputs are enabled (input one and input two are not enabled).

Truth Table

x_1	x_2	y
0	0	1
0	1	1
1	0	1
1	1	0

Mathematical Expression

A NAND operation is mathematically expressed using a bar over an AND operation:

 y = \overline{x_1 \cdot x_2}

OR Gate

An OR gate outputs a 1 if either or both inputs are enabled (if input one or input two is enabled).

Truth Table

x_1	x_2	y
0	0	0
0	1	1
1	0	1
1	1	1

Mathematical Expression

A mathematical OR is notated with a + symbol.

 y = x_1 + x_2 

NOR Gate

A NOR gate outputs a one if neither gate is enabled.

Truth Table

x_1	x_2	y_1
0	0	1
0	1	0
1	0	0
1	1	0

Mathematical Expression

A NOR operation is expressed using a bar over an OR operation.

 y = \overline{x_1 + x_2} 

XOR Gate

An XOR gate is on if one input is enabled, but not both (exclusively one or the other).

Truth Table

x_1	x_2	y
0	0	0
0	1	1
1	0	1
1	1	0

Mathematical Expression

An XOR operation is expressed using a circle around an addition symbol:

 y = x_1 \oplus x_2 

XNOR Gate

An XNOR gate is on if neither input is enabled, or both inputs are enabled.

Truth Table

x_1	x_2	y
0	0	1
0	1	0
1	0	0
1	1	1

Mathematical Expression

An XNOR operation is expressed using a bar over an XOR operation:

 y = \overline{x_1 \oplus x_2}